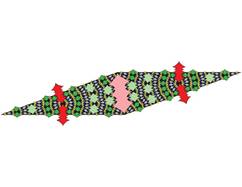
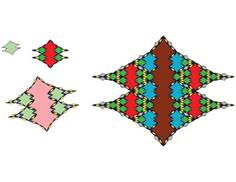
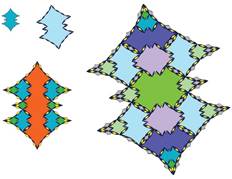
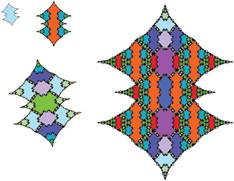
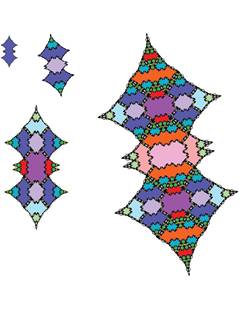
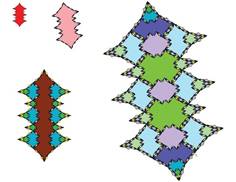
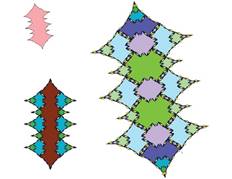
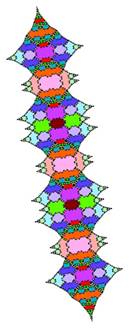
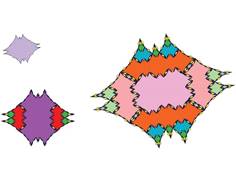
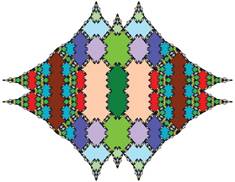
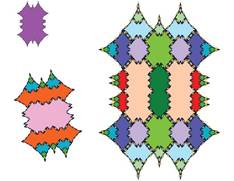
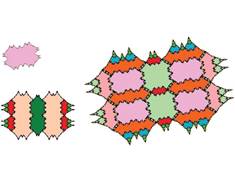
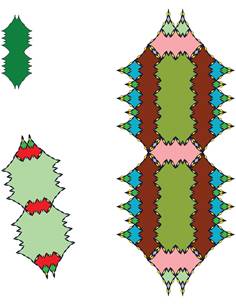
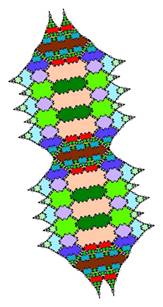
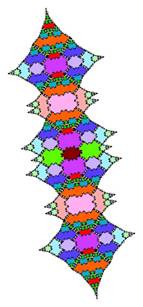
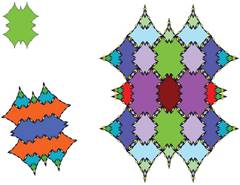
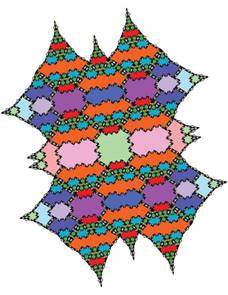
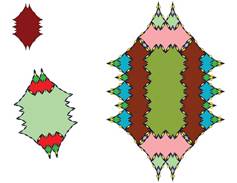
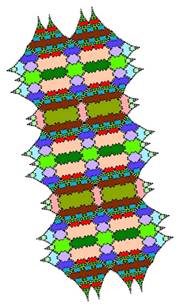
Tiling with 18-fold symmetry (n=9)
The tiling for n=9 showing 18-fold symmetry is shown below.

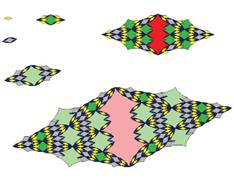
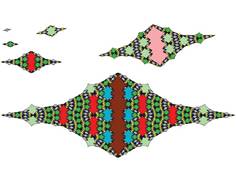
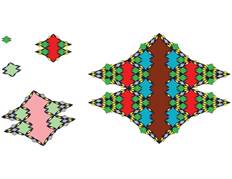
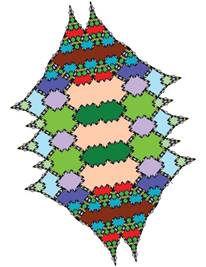
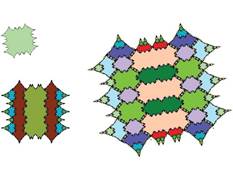
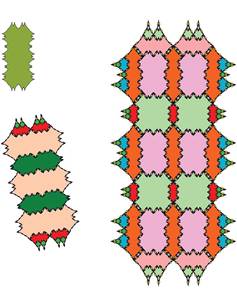
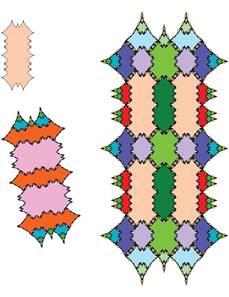
The following pictures show at least the first 3 inflations of each of the tiles.
|
Tile 1 and inflations 1-5 PDF |
Tile 1 inflation 6 PDF |
Tile 1 inflation 7 PDF |
|
Tile 2 and inflations 1-5 PDF |
Tile 2 inflation 6 PDF |
Tile 3 and inflations 1-5 PDF |
|
Tile 4 and inflations 1-4 PDF |
Tile 5 and inflations 1-3 PDF |
Tile 6 and inflations 1-3 PDF |
|
Tile 7 and inflations 1-3 PDF |
Tile 8 and inflations 1-3 PDF |
Tile 9 and inflations 1-3 PDF |
|
Tile 10 and inflations 1-2 PDF |
Tile 10 inflation 3 PDF |
Tile 11 and inflations 1-2 PDF |
|
Tile 11 inflation 3 PDF |
Tile 12 and inflations 1-2 PDF |
Tile 12 inflation 3 PDF |
|
Tile 13 and inflations 1-2 PDF |
Tile 13 inflation 3 PDF |
Tile 14 and inflations 1-2 PDF |
|
Tile 14 inflation 3 PDF |
Tile 15 and inflations 1-2 PDF |
Tile 15 inflation 3 PDF |
|
Tile 16 and inflations 1-2 PDF |
Tile 16 inflation 3 PDF |
Tile 17 and inflations 1-2 PDF |
|
Tile 17 inflation 3 PDF |
Tile 18 and inflations 1-2 PDF |
Tile 18 inflation 3 PDF |
|
Tile 19 and inflations 1-2 PDF |
Tile 19 inflation 3 PDF |
Tile 20 and inflations 1-2 PDF |
|
Tile 20 inflation 3 PDF |
Tile 21 and inflations 1-2 PDF |
Tile 21 inflation 3 PDF |
|
Tile 22 and inflations 1-2 PDF |
Tile 22 inflation 3 PDF |
|
Periodic tiles and fixed points
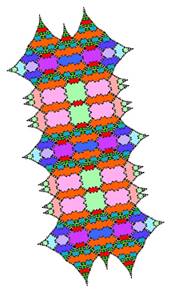
There are two sets of tiles with period 7, shown in the second row and third row of the set of prototiles at the top above. For each tile, the iteration has the next tile in its center. The last tile in each row has the first tile at its center.
There is one fixed point vertex pattern in the tiling, emerging at every vertex, where the mandala below emerges with higher iterations. This mandala was created using the fifth iteration of the thin rhomb.

Back to Filling the Gaps n-fold tiling
Copyright 2020 by Jim Millar